Cálculo de límites

Cálculo de límites 

Las funciones matemáticas se utilizan en otros ámbitos, por ejemplo, para calcular los beneficios o los costes de una empresa, la velocidad o aceleración de un móvil, etc., por lo que es importante conocer el comportamiento de una función.

Por ejemplo, la siguiente función no está definida en $x=0$ ni en $x=-1$ (porque no se puede dividir entre $0$):

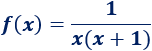
Sin embargo, sí podemos preguntarnos cómo se comporta la función cuando $x$ se aproxima a $0$ o cuando se aproxima a $-1$.  ¿Y si $x$ crece o decrece indefinidamente? Los límites de la función $f$ nos proporcionan las respuestas.

Además de ayudarnos a visualizar la gráfica de la función, los límites también se utilizan para estudiar otras propiedades, como la continuidad de una función, la diferenciabilidad, etc.

ejercicios propios:

Límites infinitos vs límites en el infinito

Límites infinitos vs límites en el infinito

Se dice que existe límite infinito cuando la función f(x) llega a valores que crecen continuamente, es decir que se puede hacer la funcio tan grande como queramos. Se dice que f(x) diverge a infinito. Para ello, el valor al que tienda la variable independiente x puede ser tanto a un número finito, como tender al infinito (limites al infinito).

Veamos un caso, con un límite infinito en la siguiente función:

Su límite cuando la variable tiende a 2 es:

Se puede comprobar si damos valores a la x cada vez más cercanos a 2, tanto acercándonos por su izquierda como por su derecha, como se ve en el siguiente cuadro, el límite tiende a +∞:

Visto en esta gráfica:

Un límite en el infinito es aquel al que tiende f(x) cuando la variable x se hace tan grande, tanto en positivo como en negativo, como queramos. Entonces la funcion f(x) puede tender a un valor finito o puede diverger a infinito (limite infinito).

Veamos un caso, con un límite en el infinito en la siguiente funcion:

Su límite cuando la variable tiende a 2 es:

Se puede comprobar si damos valores a la x cada vez más cercanos a +∞. Como se ve en el siguiente cuadro, el límite tiende a 1:

Visto en esta gráfica:

ya por ultimo vamos a ver los ejemplos propios , profe Edison espero te guste y este bien.

Nicolas Daniel Barreto Choconta 1102 Calculo